
So in short, if you have a curve, the vertical line test checks if that curve is a function, and the horizontal line test checks whether the inverse of that curve is a function. If a horizontal line cuts the curve more than once at some point, then the curve doesn't have an inverse function. So if you want to check whether a function has an inverse that is also a function, you can check whether every $y$ value has at most one $x$ value, so you use the horizontal line test. Imagine moving a vertical line throughout the graph. When you find the inverse of a function, you reflect the function by the line $y=x$, or swap the $x$ and $y$ axes. If the vertical line cuts the curve y f (x) at one distinct point, then the curve represents a function, and if it cuts at more than one distinct point, then it does not represent a function. The vertical line is parallel to the y-axis and is represented as x a. If at some point the function crosses a vertical line twice, it's telling you that there are two $y$ values for that $x$ value, so the curve is not a function. The vertical line test is useful to find if a curve represents a function or not. Explain why the vertical line test shows. If you think about it, the vertical line test is simply a restatement of the definition of a function. states that if a vertical line intersects the graph of the relation more than once, then the relation is a NOT a function. In order to be a function, each x value can. Then choose your answers from the pull-down menues. The vertical line test is used to determine whether a curve on an x y xy xy -plane is a function. is a way to determine if a relation is a function. The Vertical Line Test is a visual test that you can use to quickly check and see if a graph represents a function. The vertical line test is to check if a curve is a function. Look carefully at the graphs, and think about what the Vertical Line Test tells you. In the graph of a function, no vertical line can pass through more.

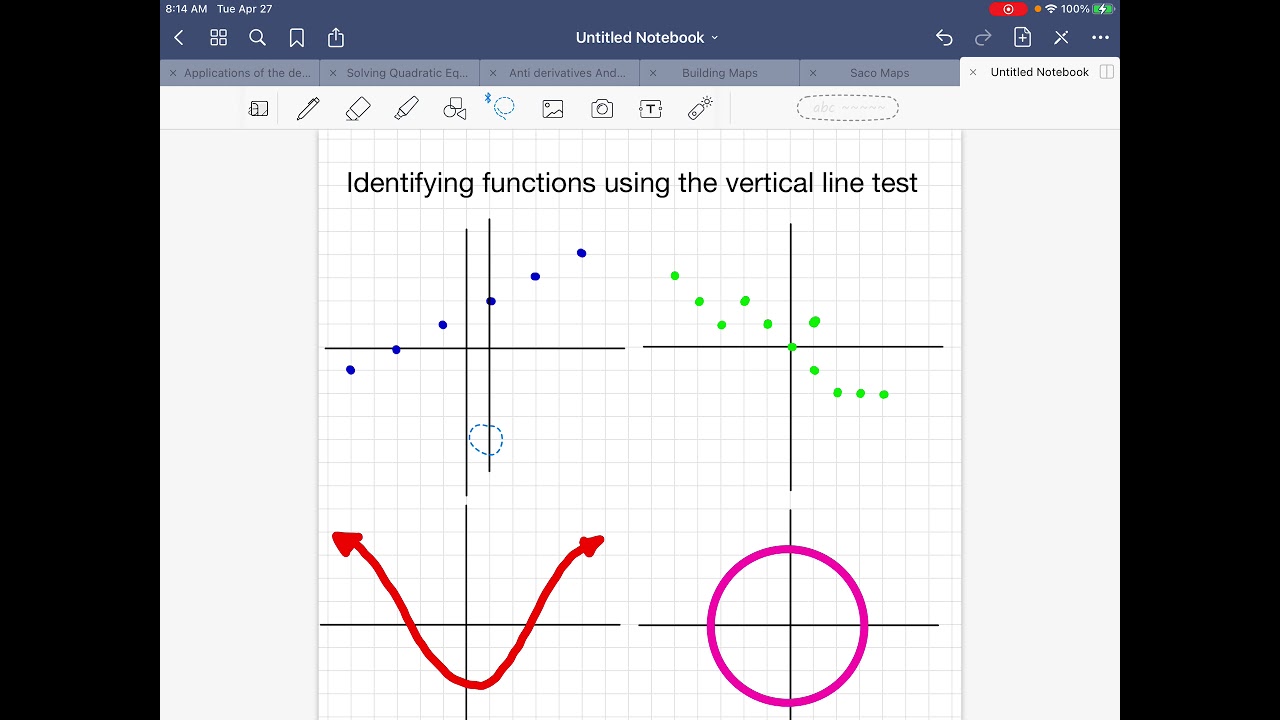
It doesn't require that every $y$ value has at most one $x$ value though, so the inverse of a function is not necessarily a function itself. A one-to-one function passes the horizontal line test as well as the vertical line test. The definition of a function requires that every $x$ value has at most one $y$ value.


 0 kommentar(er)
0 kommentar(er)
